Calcule as chances de se ganhar na loteria.
Consideremos a experiência do lançamento de uma moeda e leitura da face voltada para cima. Ao realizarmos n vezes a experiência, se obtivermos m vezes o resultado “cara” é
. É claro que lançada a moeda o resultado é imprevisível, pois não podemos dizer com absoluta certeza que o resultado será “cara”, pois nada impede que dê “coroa”.A experiência provou que conforme se aumenta n, ou seja, à medida que mais lançamentos da moeda são feitos, a frequência relativa
tende a estabilizar-se em torno de 
.Exemplo:
Em 1000 lançamentos (n = 1000), 529 resultados foram favoráveis (m = 529), o que nos dá para
o valor de 0,529.Em 4040 lançamentos, 2048 resultados foram favoráveis o que nos da
= 0,50693, isso significa que no lançamento de uma moeda “honesta” a probabilidade de se obter “cara” é 
. Essa experiência foi realizada por Kerrich e Buffon.A definição que permite calcular teoricamente a probabilidade de um evento, sem realizar a experiência é:
Dado um espaço amostral S, com n (S) elementos, e um evento a de S, com n(A) elementos, a probabilidade do evento A é o P(A) tal que:
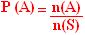
Propriedades
Sendo S ≠
um espaço amostral qualquer, A um evento de S e 
o complementar de A em S, valem as seguintes propriedades:? P(
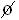) = 0? P(S) = 1
? 0 ≤ P(A) ≤ 1
? P(A) + P(
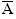) =1Por Danielle de Miranda
Graduada em Matemática
